빰_s
(25.02.16) 힙, 우선순위 큐의 개념과 사용 본문
1. 힙이란?
완전 이진 트리의 일종으로써, 여러 값들 중 최대값(Max)와 최솟값(Min)을 빠르게 찾아낼 수 있도록 만들어진 이진트리
여기서 완전 이진 트리란, 모든 레벨이 꽉 찬 이진트리를 의미하며,
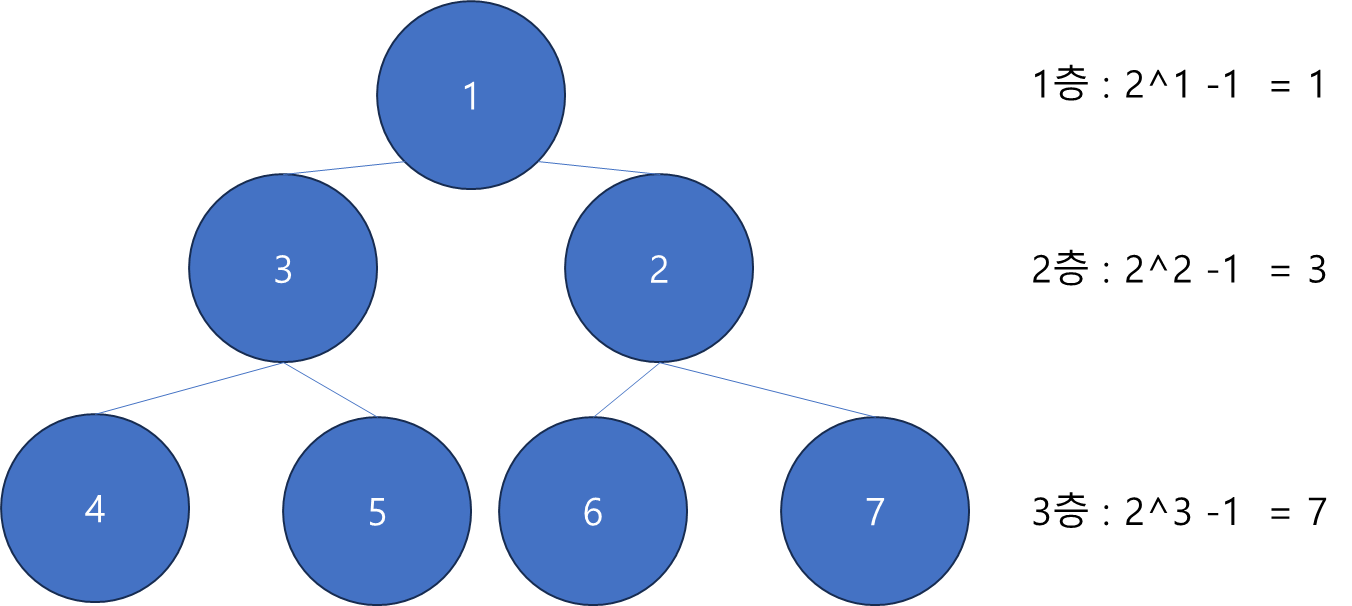
이 완전 이진 트리가 가지는 모든 노드의 수는 층 수에 따라 2의 (층수) 제곱 -1로 정의된다.
(ex. 2층의 경우 총 노드의 수는 3개(2^2 -1), 3층의 경우 총 노드의 수는 7개(2^3-1)로써, 각 층별로 2의 제곱수가 된다.)
2. 특징
일반적으로 힙을 만들 때, 우선순위 큐를 사용하기 위해 만들어지며 이는 최대 힙, 최소힙으로 보통 정의된다. 최대 힙과 최소 힙이 뭔지 설명하기 전에 우선순위 큐에 대해 먼저 알고 넘어가보자.
- 우선순위 큐 : 우선순위의 개념을 큐에 도입한 자료구조로써, 데이터들이 각기 우선순위를 가지고 있으몀, 우선순위가 높은 데이터가 먼저 출력되는 구조를 가진다.
(※ 스택은 LIFO(후입선출), 큐는 FIFO(선입선출)의 구조)
또한 우선순위 큐는 배열,연결 리스트(Linked List), 힙으로 구현 가능하며 이 중에선 힙을 이용한 작성이 가장 효율적이라 볼 수 있다.
다시 힙으로 넘어오자면, 힙은 반정렬 상태의 구조를 가지며, 중복된 값을 허용한다. 같은 값이 있어도 우선순위 큐의 정렬 로직에는 해를 끼치지 않기 때문에 큰 문제가 없기 때문이다.(이후 그보다 작은 값이 들어오면 자동적으로 정렬이 진행될테고.. 다만, 일반적인 이진 탐색 트리는 중복값을 허용하지 않는다)
마지막으로, 앞서 언급했던 최대 힙과 최소 힙의 정의를 간단히 정의하자면,
- 최대 힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리
- 최소 힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진트리
즉 최대 힙은 큰 값이 우선순위를 가지는 구조, 최소 힙은 작은 값이 우선순위를 가지는 구조라고 볼 수 있다.
3. 힙의 사용
- 부모 노드와 자식 노드의 관계
왼쪽 자식의 인덱스 : (부모 노드의 인덱스) * 2
오른쪽 자식의 인덱스 : (부모 노드의 인덱스) * 2 -1
부모 인덱스 : (지식 노드의 인덱스) /2
- 힙의 삽입
새로운 요소가 들어오게 되면, 힙의 마지막 노드에 삽입되며, 그 새로운 노드를 최소힙/최대힙 등의 조건에 맞춰 부모 노드들과 위치를 교환해가며 완전 이진 트리를 재정의한다.
- 힙의 삭제
힙에서 요소 삭제 시 루트 노드가 삭제되며, 우선순위 큐의 구조에 따라 최대 힙의 경우엔 최댓값이, 최소 힙의 경우엔 최솟값이 삭제된다.
삭제된 루트 노드에선 남은 노드들 중에서 가장 큰 우선순위를 가지는 노드를 루트 노드로 재정의한 후, 완전 이진 트리를 재정의하여 힙을 재구성하게 된다.
'Java' 카테고리의 다른 글
| (25.01.26) Comparator VS Comparable (0) | 2025.01.27 |
|---|---|
| (25.01.05) Array vs ArrayList vs LinkedList (0) | 2025.01.05 |
| [Java] 소숫점 자릿수만큼 출력하는 방법 (0) | 2024.01.01 |
| (2023.02.02) 객체지향 설계 원칙(S O L I D) (0) | 2023.02.02 |
| (22.07.27) String vs StringBuffer vs StringBuilder (2) | 2022.07.27 |

